有限元法(Finite Element Method, FEM)是一种将连续体视为若干个有限大小的单元 体的离散化集合,以求解连续体热、力、电磁问题的数值方法,其基本思想是将连续的求解区域离散为一组有限个、且按一定方式
相互连接在一起的单元的组合体。适合的研究方向包括但不限于:机械、土木、工艺、工业、工程、光学、声学等。
常用软件:Comsol,Ansys,Abaqus,Fluent等。
有限元定义
在数学中,有限元法(FEM,Finite Element Method)是一种为求解偏微分方程边值问题近似解的数值技术。求解时对整个问题区域进行分解,每个子区域都成为简单的部分,这种简单部分就称作有限元。它通过变分方法,使得误差函数达到最小值并产生稳定解。类比于连接多段微小直线逼近圆的思想,有限元法包含了一切可能的方法,这些方法将许多被称为有限元的小区域上的简单方程联系起来,并用其去估计更大区域上的复杂方程。它将求解域看成是由许多称为有限元的小的互连子域组成,对每一单元假定一个合适的(较简单的)近似解,然后推导求解这个域总的满足条件(如结构的平衡条件),从而得到问题的解。这个解不是准确解,而是近似解,因为实际问题被较简单的问题所代替。由于大多数实际问题难以得到准确解,而有限元不仅计算精度高,而且能适应各种复杂形状,因而成为行之有效的工程分析手段。
有限元应用范围:固体力学、流体力学、热传导、电磁学、声学、生物力学
有限元求解情况:杆、梁、板、壳、块体等各类单元构成的弹性(线性和非线性)、弹塑性或塑性问题(包括静力和动力问题)。能求解各类场分布问题(流体场、温度场、电磁场等的稳态和瞬态问题),水流管路、电路、润滑、噪声以及固体、流体、温度相互作用的问题。
可计算内容
1.电磁相关仿真,电场、磁场、电磁耦合、磁热耦合、电机、射频微波等。
2.结构相关仿真,接触分析、非线性分析、振动、疲劳、传热、裂纹、碰撞分析等。
3.流体相关仿真,多相流体、导热换热散热、组分运输、流体流动、相变、管道阻力等。
4.光学、声学仿真等。
常见计算内容
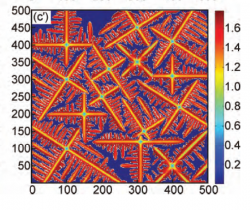
多个等轴晶生长形貌及溶质浓度分布
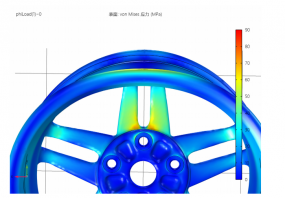
结构力学-轮毂受力分析
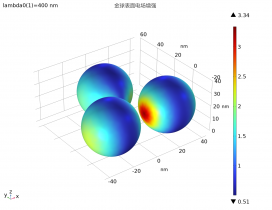
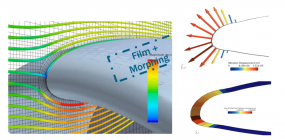
有限元光学近电场分析
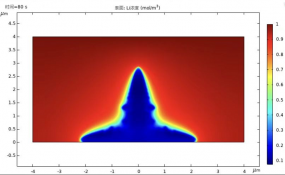
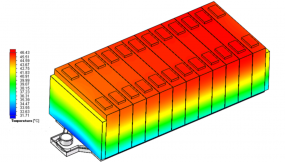
锂电池热管理系统
多相流流动
电化学-离子浓度分布
光学-镜头光路模拟
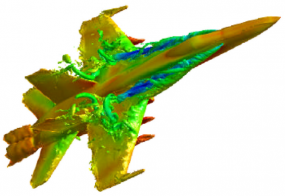
计算流体力学-气动性能计算
计算流体力学-热传递分析
计算流体力学-多相流动分析
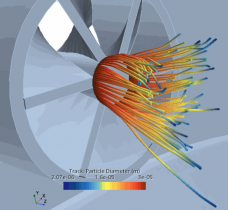
计算流体力学-颗粒流
计算流体力学-燃烧反应流
计算流体力学-气动声学
固体力学分析
材料制造过程模拟